
Author Ryan Chadwick
It's logical really.
We'll start off by covering what exactly Boolean Algebra is and then look at some of the basic building blocks, also referred to as operators. It may seem a little abstract at this stage but once you've worked through this section and the next it will start to make a bit more sense.
Now let's evaluate some expressions.
Boolean Algebra is a way of formally specifying, or describing, a particular situation or procedure. We use variables to represent elements of our situation or procedure. Variables may take one of only two values. Traditionally this would be True and False. So for instance we may have a variable X and state that this represents if it is raining outside or not. The value of X would be :
What you have to remember is that although many things in the real world exist on a spectrum, in Boolean Algebra things are reduced to black and white. So we could have, for instance, light rain, steady rain, or heavy rain. In Boolean Algebra however, it is either raining or it isn't. This may seem a little limiting but this simplification of things actually turns out to be quite powerful.
It is possible to substitute other values in place of True and False. When working with computers it is often the case that True and False is replaced with 1 and 0. When working with physical circuits we may replace True and False with the presence or absence of a voltage.
In this way Boolean Algebra is useful to describe a process and then to build mechanisms which can perform those processes. Keep this in mind as you're working through the next few sections. This is what we are building towards.
For the single variable functions may exist only four different Boolean functions g1, g2, g3 and g4, presented in the following table:
| X | g1 | g2 | g3 | g4 |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
It follows from the table that the functions g1 and g4 do not depend on the argument and are, respectively, constants 0 and 1, and the function g2 repeats the value of the argument, i.e. g2 = x. The function g3 is called the negation or inverse of the variable x and is denoted not (x).
For functions of two variables, there can be 16 (and only 16) different functions. The truth table of these functions is as follows:
| X | Y | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | AND conjunction | ban on y | 0 | ban on x | 0 | mod 2 addition | OR disjunction | Pierce's | equivalence | 1 | implication | 1 | implication | Schaeffer's | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
These functions include 6 degenerate functions (constants: F0 = 0 and F15 = 1; variables: F3 = x1 and F5 = x2; inversions: F12 = not x1 and F10 = not x2).
We saw above that variables may be used to represent the current state of elements that we are interested in. Operations allow us to then define relationships between those variables. There are three basic operations. These are used often in Boolean expressions but are also used to create more complex operations. You'll probably find that you've actually used these operations quite a bit, you've just never thought of them formally before.
The result of an operation is similar to variables, it may only be either True or False.
I have chosen to always write operations in all UPPERCASE. This is so they are easily identified as operations. Many people follow this convention but it is not required. Feel free to use whatever method suits you best.
The first operation is AND and it means pretty much what it does in plain english. So for instance I may state "If it's sunny outside AND I have completed my work then I will go for a run." To represent this in Boolean Algebra I may say that:
And I would write it like so:
x AND y = z
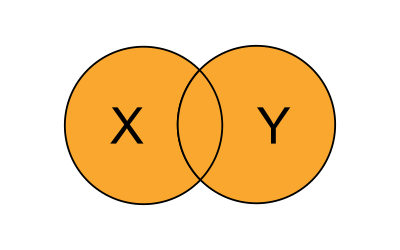
Here it is represented visually. The shaded region is the region which represents AND.

And now we'll represent it using what is called a Truth table. A truth table lists all the possible combinations of inputs for an expression (in this case a single operation) and what the result, or output should be.
| X | Y | Result |
|---|---|---|
| False | False | False |
| True | False | False |
| False | True | False |
| True | True | True |
OR is also the same as how we would use it in plain english. It means that if either of the two variables is True then the result is True. So for instance I could say that "I will get home early from work if I get to leave early OR the traffic is good".
Here is OR represented visually :
And again as a truth table :
| X | Y | Result |
|---|---|---|
| False | False | False |
| True | False | True |
| False | True | True |
| True | True | True |
Note that AND is False for all but True and True whilst OR is True for all but False and False. This observation will become useful to us later on. In fact there are many shortcuts and advantageous benefits to be gained from finding patterns like this so keep an eye out for them.
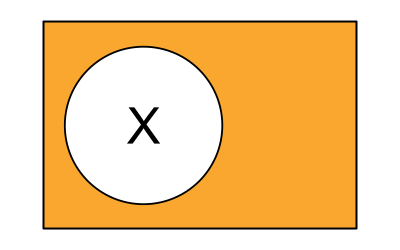
Not is quite similar to how we use it in plain english. It has a subtle difference when used in Boolean Algebra. Normally I might say something like "I will eat dessert if I am not full". I could also have said "I will eat dessert if I am still hungry", which has the same meaning but using an opposite value. So not actually has the effect of flipping the value of a variable. If :
Represented visually that is :
And as a truth table :
| X | Result |
|---|---|
| True | False |
| False | True |
The above three operations are the building blocks for just about everything else we can do in Boolean Algebra. We will now introduce what are called derived operations. These are essentially shortcuts for commonly used combinations of the basic operations. As we will discover later on, some of these derived operations are very useful when we want to do computations and other things.
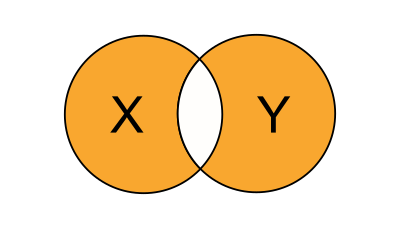
With the operation OR we saw that as long as one of the variables is True the result is True. It was also True if both of them were True. With the operation XOR we now say that the result will be True only if one of the two variables is True. That is, one of them is True but only one of them is True. We may build this operation from the basic operations like so :
g XOR p is equivalent to (g OR p) AND NOT(g AND p)
When brackets ( ) are used in an expression this means that we evaluate that part of the expression first before the other parts.
Let's run through an example to better understand what's going on.
If g is True and p is False then :
Substituting g and p for those values we get :
(True OR False) AND NOT(True AND False)
The first set of brackets (True OR False) AND NOT(True AND False) evaluates to True so let's replace that into the expression and we get :
True AND NOT(True AND False)
The next set of brackets True AND NOT(True AND False) evaluates to False so let's replace that into the expression as well giving us :
True AND NOT(False)
NOT(False) evaluates to True so we can apply that to the expression and we end up with :
True and True
And the final result is True.
Visually XOR looks like :
XOR as a truth table :
| X | Y | Result |
|---|---|---|
| False | False | False |
| True | False | True |
| False | True | True |
| True | True | False |
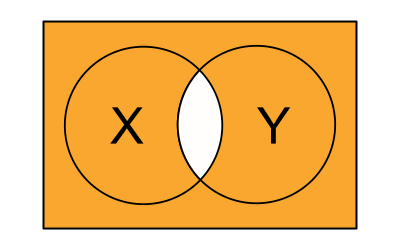
NAND is effectively the opposite of what AND is.
r NAND S is equivalent to NOT(r AND s)
Visually it looks like this :
NAND as a truth table :
| X | Y | Result |
|---|---|---|
| False | False | True |
| True | False | True |
| False | True | True |
| True | True | False |
NOR is effectively the opposite of OR.
b NOR k is equivalent to NOT(b OR k)
Visually it looks like this :
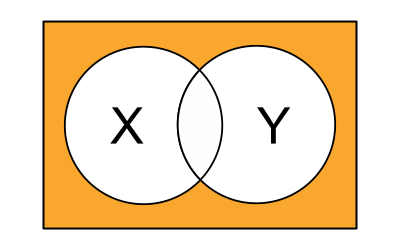
NOR as a truth table :
| X | Y | Result |
|---|---|---|
| False | False | True |
| True | False | False |
| False | True | False |
| True | True | False |